Công thức tính diện tích hình thoi, chu vi hình thoi kèm 15 ví dụ hay

Để tính diện tích hình thoi và chu vi hình thoi thì bạn cần biết định nghĩa và công thức tính toán. Hình thoi là một hình học có bốn cạnh bằng nhau và hai đường chéo vuông góc với nhau. Với kiến thức này, bạn có thể dễ dàng tính toán diện tích và chu vi của hình thoi. Hãy cùng tìm hiểu thêm về tính diện tích, chu vi hình thoi và ứng dụng của nó trong cuộc sống hàng ngày.

Hình thoi là gì?

Hình thoi (hay còn được gọi là hình tháp kim cương) là một hình học phẳng có bốn cạnh bằng nhau và hai đường chéo có độ dài bằng nhau nhưng không vuông góc với nhau. Hình thoi có hai góc đối diện nhau là góc bù và hai góc đối diện còn lại là góc nhọn. Hình thoi là một trong số các hình học cơ bản và có nhiều ứng dụng trong đại số, hình học và thực tế, ví dụ như trong thiết kế kim cương, hình thành các hình dạng và đường đi trong các trò chơi, hay trong các bài toán hình học về diện tích, chu vi, và khoảng cách giữa các điểm trên mặt phẳng.

Tính chất của hình thoi 

Dưới đây là một số tính chất cơ bản của hình thoi:

1. Các cạnh của hình thoi bằng nhau: Hình thoi có bốn cạnh bằng nhau, do đó độ dài của các cạnh là như nhau.
2. Hai đường chéo của hình thoi bằng nhau: Hai đường chéo của hình thoi cắt nhau ở góc vuông và có độ dài bằng nhau.
3. Hình thoi có đối xứng trục: Hình thoi có đối xứng trục qua trung điểm của hai đường chéo.
4. Hình thoi có đối xứng trung tâm: Hình thoi có đối xứng trung tâm, với trung tâm nằm ở giao điểm của đường chéo.
5. Hình thoi có góc bù: Hai góc đối diện của hình thoi là góc bù.
6. Hình thoi có tổng bốn góc bằng 360 độ: Tổng bốn góc của hình thoi luôn bằng 360 độ.
7. Hình thoi có diện tích là nửa tích chéo: Diện tích của hình thoi là bằng nửa tích chéo lớn nhất nhân với tích chéo bé nhất.
8. Hình thoi có chu vi là tổng bốn cạnh: Chu vi của hình thoi là tổng độ dài của bốn cạnh.

Các tính chất này rất hữu ích trong việc giải quyết các bài toán liên quan đến hình thoi.

Các dấu hiệu nhận biết hình thoi

Dưới đây là một số dấu hiệu nhận biết hình thoi trên mặt phẳng:

1. Các cạnh bằng nhau: Hình thoi có bốn cạnh bằng nhau, do đó nếu bạn có một hình học có bốn cạnh đều bằng nhau, có thể nó là một hình thoi.
2. Hai đường chéo bằng nhau: Hai đường chéo của hình thoi có độ dài bằng nhau, do đó nếu bạn có một hình học mà hai đường chéo có độ dài bằng nhau, có thể nó là một hình thoi.
3. Góc vuông giữa hai đường chéo: Hai đường chéo của hình thoi cắt nhau tại góc vuông, do đó nếu bạn có một hình học mà hai đường chéo cắt nhau tại góc vuông, có thể nó là một hình thoi.
4. Hai góc đối diện bù nhau: Hai góc đối diện của hình thoi là góc bù (lớn hơn 90 độ), do đó nếu bạn có một hình học mà hai góc đối diện lớn hơn 90 độ và bằng nhau, có thể nó là một hình thoi.
5. Điểm giao nhau của các đường chéo là trung điểm: Hình thoi có điểm giao nhau của các đường chéo là trung điểm của chúng, do đó nếu bạn có một hình học mà điểm giao nhau của hai đường chéo là trung điểm, có thể nó là một hình thoi.

Tóm lại, để nhận biết một hình học có phải là hình thoi hay không, bạn cần kiểm tra các tính chất của hình thoi như cạnh bằng nhau, hai đường chéo bằng nhau, góc vuông giữa hai đường chéo, hai góc đối diện bù nhau và điểm giao nhau của các đường chéo là trung điểm.

Công thức tính chu vi hình thoi kèm 5 ví dụ

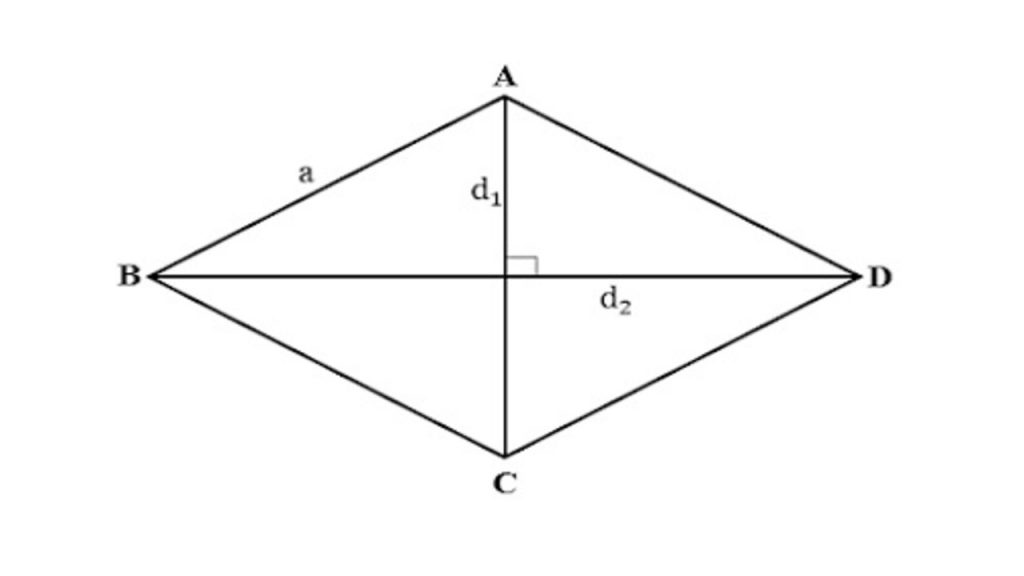
Công thức tính chu vi của hình thoi là: chu vi = 4 X độ dài cạnh = 4 X a

Ví dụ:

1. Hình thoi có độ dài cạnh là 8cm, tính chu vi của hình thoi. Chu vi = 4 x 8cm = 32cm
2. Hình thoi có độ dài cạnh là 10m, tính chu vi của hình thoi. Chu vi = 4 x 10m = 40m
3. Hình thoi có độ dài cạnh là 5.2cm, tính chu vi của hình thoi. Chu vi = 4 x 5.2cm = 20.8cm
4. Hình thoi có độ dài cạnh là 15mm, tính chu vi của hình thoi. Chu vi = 4 x 15mm = 60mm
5. Hình thoi có độ dài cạnh là 3.5m, tính chu vi của hình thoi. Chu vi = 4 x 3.5m = 14m

Như vậy, để tính chu vi của hình thoi, bạn cần nhân độ dài cạnh với 4. Công thức này rất đơn giản và dễ dàng để tính toán chu vi của hình thoi.

Công thức tính diện tích hình thoi kèm 5 ví dụ

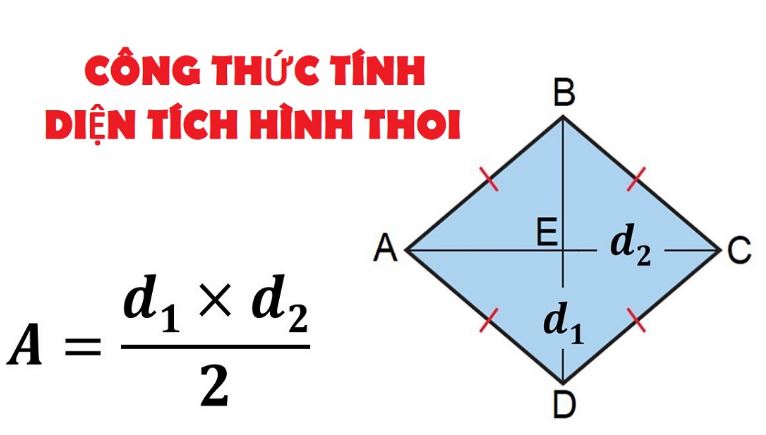
Công thức tính diện tích hình thoi là: diện tích = độ dài đường chéo dài x độ dài đường chéo ngắn / 2.

Ví dụ:

1. Hình thoi có đường chéo dài 10cm và đường chéo ngắn 8cm, tính diện tích của hình thoi. Diện tích = 10cm x 8cm / 2 = 40cm²
2. Hình thoi có đường chéo dài 15m và đường chéo ngắn 9m, tính diện tích của hình thoi. Diện tích = 15m x 9m / 2 = 67.5m²
3. Hình thoi có đường chéo dài 6.4cm và đường chéo ngắn 4.8cm, tính diện tích của hình thoi. Diện tích = 6.4cm x 4.8cm / 2 = 15.36cm²
4. Hình thoi có đường chéo dài 12mm và đường chéo ngắn 8mm, tính diện tích của hình thoi. Diện tích = 12mm x 8mm / 2 = 48mm²
5. Hình thoi có đường chéo dài 5.6m và đường chéo ngắn 3.2m, tính diện tích của hình thoi. Diện tích = 5.6m x 3.2m / 2 = 8.96m²

Như vậy, để tính diện tích của hình thoi, bạn cần nhân độ dài đường chéo dài với độ dài đường chéo ngắn, sau đó chia kết quả cho 2. Công thức này cũng rất đơn giản và dễ dàng để tính toán diện tích của hình thoi.

5 ví dụ phức tạp hơn tính chu vi và diện tích hình thoi kèm lời giải chi tiết

Đây là 5 ví dụ tính chu vi và diện tích hình thoi phức tạp hơn:

1. Cho hình thoi ABCD với đường chéo dài 16cm và đường chéo ngắn 8cm. Tính chu vi và diện tích của hình thoi.

Lời giải: Trước tiên, ta cần tìm độ dài cạnh của hình thoi. Ta biết rằng hình thoi là một hình bình hành, vì vậy cạnh của hình thoi có độ dài bằng với một nửa đường chéo ngắn. Vậy cạnh của hình thoi là 4cm.

Bây giờ, ta có thể tính chu vi và diện tích của hình thoi bằng công thức:

• Chu vi = 4 x 16cm = 64cm
• Diện tích = 16cm x 8cm / 2 = 64cm²

Vậy chu vi của hình thoi là 64cm, diện tích của hình thoi là 64cm².

2. Cho hình thoi ABCD có cạnh 12cm và một góc bằng 60 độ. Tính chu vi và diện tích của hình thoi.

Lời giải: Để tính chu vi của hình thoi, ta cần biết độ dài cạnh của hình thoi. Vì ta biết một góc bằng 60 độ, ta có thể sử dụng định luật sine để tìm độ dài cạnh của hình thoi: sin 60° = cạnh đối diện / đường chéo cạnh đối diện = sin 60° x đường chéo cạnh đối diện = 0.866 x 12cm cạnh đối diện ≈ 10.392cm

Bây giờ, ta có thể tính chu vi và diện tích của hình thoi bằng công thức:

• Chu vi = 4 x 12cm = 48cm
• Diện tích = 10.392cm x 12cm / 2 = 62.352cm²

Vậy chu vi của hình thoi là 48cm, diện tích của hình thoi là 62.352cm².

3. Cho hình thoi ABCD có đường chéo dài 10cm và một cạnh dài 8cm. Tính chu vi và diện tích của hình thoi.

Lời giải: Để tính độ dài đường chéo ngắn của hình thoi, ta có thể sử dụng định lý Pythagoras: đường chéo ngắn² = đường chéo dài² – cạnh² đường chéo ngắn² = 10cm² – 8cm² đường chéo ngắn² = 36cm² đường chéo ngắn = √36cm² đường chéo ngắn = 6cm

Bây giờ, ta sẽ có :

• Chu vi = 2 x (8cm + 6cm) = 28cm
• Diện tích = 8cm x 6cm = 48cm²

Vậy chu vi của hình thoi là 28cm, diện tích của hình thoi là 48cm².

4. Hình thoi ABCD có đường chéo dài 18cm và góc giữa hai đường chéo bằng 120 độ. Tính chu vi và diện tích của hình thoi.

Lời giải: Ta cần tìm độ dài cạnh của hình thoi trước khi tính chu vi và diện tích. Sử dụng định luật cosine, ta có thể tìm độ dài của một nửa đường chéo ngắn: cos 60° = cạnh đối diện / đường chéo dài cạnh đối diện = cos 60° x 18cm cạnh đối diện = 9cm

Do đó, độ dài một cạnh của hình thoi là 9cm.

• Chu vi = 4 x 9cm = 36cm
• Diện tích = 9cm x 18cm / 2 = 81cm²

Vậy chu vi của hình thoi là 36cm, diện tích của hình thoi là 81cm².

5. Hình thoi ABCD có đường chéo dài 20cm và một góc bằng 45 độ. Tính chu vi và diện tích của hình thoi.

Lời giải: Tìm độ dài cạnh của hình thoi:

• Theo định luật sine: sin 45° = cạnh đối diện / đường chéo
• cạnh đối diện = sin 45° x 20cm
• cạnh đối diện ≈ 14.142cm
• Chu vi = 4 x 14.142cm ≈ 56.568cm
• Diện tích = 20cm x 20cm / 2 ≈ 200cm²

Vậy chu vi của hình thoi là khoảng 56.568cm, diện tích của hình thoi là khoảng 200cm².